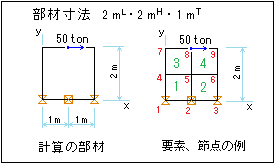
四角形4節点要素、補足説明
節点・応力値の配置
(大小順位) →図表
rev.2012-2-3 org.2010-6-8 Mori Design Office
2次元・有限要素法による応力解析に関し、任意の四角形4節点要素に対し、ガウス積分点を4点とする応力値が算出されているとする。
即ち、要素節点数4個に対し、積分点の応力値4個が得られている。この積分点の応力値を並び換えて節点の応力に割り当てる。
及び、このプログラム(Javascript)を記載する。 これを応力解析に追加すれば、節点に平滑な分布で応力値を配設できる。
但し、集中荷重直下では応力分布が不連続となるので配慮が必要。→節点・応力値の配置(追加処理)
備考
任意の要素において、節点変位uの値は、節点への力 Fを既知として、F= K・u より求められ、ここに剛性 K(=t∫BTDB dA)は
ガウスの求積にて
K ≒ tΣNBkT D Bk・det(J)k=1 但し、積分点の個数 N=4 とする ----式(1)
なお、tは厚み、B, D, det(J)は「四角形4節点要素」の説明の式(2-2),(3-1)(3-2),(6-1)を参照、
積分点N=4 は二重積分でのガウス積分n=2 を参照。
ひずみε および 応力σは、式(1)でのガウスの積分点を用いて、
εk = Bku σk = D Bk u 但し、k=1,2,3,4 ----式(2)
従って、算出されるひずみ値および応力値は各々4個づつとなる。なお、この積分点1~4の番号の付方は任意となっている。
積分点は、要素節点と対応関係がない。応力値の分布は平滑であるとして、近似的に対応させる方法を下記に記載する。
|
○冒頭の通り、要素節点数と同数4個の積分点に対し、応力が算出さてれているとし、本記載プログラムにそくして、以下説明する。
①前提:要素No,要素節点Noの位置に於ける、節点Noを配列NodNoで得る。 節点No = NodNo[要素No,要素節点No]
②前提:要素No,積分点Noの位置に於ける、応力値を配列σx,σy,τxyで得る。例えば、σx値 = σx[要素No,要素節点No]
③任意の要素の応力は、その積分点4つの応力の平均とし、配列 σx_av,σy_av,τxy_avとし、例えば、要素σx値 = σx_av[要素No]
④要素Aに対して、隣接する要素をB,Cの2個抽出(最初の抽出をB、2番目のをC)する。なお、隣接では、共通の節点が2箇所ある。
⑤その隣接点が、要素Aに於いて要素節点No1~4の何れなのかを記憶する。Bとの隣接点 j11,j12、Cとの隣接点 j21,j22
⑥分布の平滑化を重視する事とし、並び換えは応力σx,σy,τxyのそれぞれ行う。
⑦要素Aの4積分点について、応力を大きい順に順位を付け、その順位に対する応力値を配列g2にて、応力値=g2[順位]
⑧要素Aの4節点について、③④⑤より、節点応力値の配置「図表」にて、応力値の大小の順位が定まる。
⑨節点4個に対し、⑧で得られた応力値の大小順位に、積分点の応力値4個を配設する。
|
<html><head>
<title>節点応力-HP</title>
<SCRIPT Language='JavaScript'>
<!---
//----条件データ例-----
//配列値の説明:節点番号=i、n=要素番号、k=四角形要素内の節点番号=kとすれば
//節点i=NodNo[(n-1)*4+k]、応力=σx_org[(n-1)*4+k]、x方向内力=fx[i]、x位置 = x[i]
//本例での単位:位置[m]、内力[ton]、応力[ton/m2]、但し部材厚を1m とする
//①節点番号 (Array最初の0はダミー、要素No1の節点Noは1,2,5,4)
NodNo = new Array(0,1,2,5,4,2,3,6,5,4,5,8,7,5,6,9,8);
NELT = 4;//要素の総数
x = [0,0,1,2,0,1,2,0,1,2]; y = [0,0,0,0,1,1,1,2,2,2]; //節点位置
//②処理前の節点応力値
σx_org = new Array(0,-167,-268,-86,15,268,167,-15,86,49,21,203,232,-21,-49,-232,-203);
σy_org = new Array(0,630,124,161,667,-124,-630,-667,-161,195,54,90,232,-54,-195,-232,-90);
τxy_org = new Array(0,265,338,135,62,338,265,62,135,192,265,208,135,265,192,135,208);
σx = new Array();
σy = new Array();
τxy = new Array();
for(k=1;k<=(NELT*4);k++){
σx[k] = σx_org[k];
σy[k] = σy_org[k];
τxy[k] = τxy_org[k];
}
function Node_Stress(){
//③要素についての応力(積分点4か所の応力の平均)
σx_av = new Array();
σy_av = new Array();
τxy_av = new Array();
for( ne=1;ne<=NELT;ne++){
sigx = 0; sigy = 0; tauxy = 0;
for( kk=1;kk<=4;kk++){
sigx += σx[(ne-1)*4+kk]/4;
sigy += σy[(ne-1)*4+kk]/4;
tauxy += τxy[(ne-1)*4+kk]/4;
}
σx_av[ne] = sigx;
σy_av[ne] = sigy;
τxy_av[ne] = tauxy;
}
|
|
var ne1,nee1,n1,n2;
for(ne=1;ne<=NELT;ne++){
//④隣接する要素の抽出
nn = ne+1; aN = 0;aN2 = 0;
ne1 = ne;
for(nee=1;nee<=NELT;nee++){
nee1 = nee;
if(nee1!=ne1){
for(j=1;j<=4;j++){
j1 = j;
j2 = j+1;
if(j1==4){j2 = 1;}
j3 = NodNo[(ne-1)*4+j];
j4 = NodNo[(ne-1)*4+j2];
for(i=1;i<=4;i++){
i1 = i;
i2 = i+1;
if(i1==4){i2 = 1;}
i3 = NodNo[(nee-1)*4+i];
i4 = NodNo[(nee-1)*4+i2];
if((j3==i3 && j4==i4)||(j3==i4 && j4==i3)){
aN ++;
if(aN==1){aN2 = aN; j11 = j1; j12 = j2; n1 = nee; //⑤隣接点の記憶
}
if(aN>=2&&(j12==j1||j11==j2)){aN2 = aN; j21 = j1; j22 = j2; n2 = nee; //⑤隣接点の記憶
}
aN = aN2;
}
}
}
}
}
if(aN>=2){ //④Aに対する隣接要素B,C
//⑥応力σxについて
aA = σx_av[ne]; aB = σx_av[n1]; aC = σx_av[n2];
for(i=1;i<=4;i++){g1[(i-1)] = σx[(ne-1)*4+i];}
MaxA(); //⑦
//⑧ 図表らん(2)
if( Math.abs(aB- aA)< Math.abs(aC- aA)){
a = g2[1]; g2[1]= g2[2]; g2[2] =a;
}
j23 = j22 +1; if(j22>3){j23 = j22 +1-4;}
j13 = j12 +1; if(j12>3){j13 = j12 +1-4;}
j14 = j12 +2; if(j12>2){j14 = j12 +2-4;}
//⑧ 図表らん(1)上
if( (j12==j21 && aC<(aA-Math.abs(aA*0.0000001))) || (j11==j22 && aC>(aA+Math.abs(aA*0.0000001))) ){
k1 = 0; k2 = 0; // 図表らん(3)
if(aB<aA){ k1 = 2; k2 = 2-4; } // 図表らん(4)
//⑨大小関係・図表の順位に並び換え
σx[(ne-1)*4+j11] = g2[0 + k1];
σx[(ne-1)*4+j12] = g2[1 + k1];
σx[(ne-1)*4+j13] = g2[3 + k2];
σx[(ne-1)*4+j14] = g2[2 + k2];
}
//⑧ 図表らん(1)下
if( (j12==j21 && aC>(aA+Math.abs(aA*0.0000001))) || (j11==j22 && aC<(aA-Math.abs(aA*0.0000001))) ){
k1 = 0; k2 = 0; // 図表らん(3)
if(aB<aA){ k1 = 2; k2 = 2-4; } // 図表らん(4)
//⑨大小関係・図表の順位に並び換え
σx[(ne-1)*4+j11] = g2[1 + k1];
σx[(ne-1)*4+j12] = g2[0 + k1];
σx[(ne-1)*4+j13] = g2[2 + k2];
σx[(ne-1)*4+j14] = g2[3 + k2];
}
//⑥応力σyについて
aA = σy_av[ne]; aB = σy_av[n1]; aC = σy_av[n2];
for(i=1;i<=4;i++){g1[(i-1)] = σy[(ne-1)*4+i];}
MaxA(); //⑦
//⑧ 図表らん(2)
if( Math.abs(aB- aA)< Math.abs(aC- aA)){
a = g2[1]; g2[1]= g2[2]; g2[2] =a;
}
j23 = j22 +1; if(j22>3){j23 = j22 +1-4;}
j13 = j12 +1; if(j12>3){j13 = j12 +1-4;}
j14 = j12 +2; if(j12>2){j14 = j12 +2-4;}
//⑧ 図表らん(1)上
if( (j12==j21 && aC<(aA-Math.abs(aA*0.0000001))) || (j11==j22 && aC>(aA+Math.abs(aA*0.0000001))) ){
k1 = 0; k2 = 0; // 図表らん(3)
if(aB<aA){ k1 = 2; k2 = 2-4; } // 図表らん(4)
//⑨大小関係・図表の順位に並び換え
σy[(ne-1)*4+j11] = g2[0 + k1];
σy[(ne-1)*4+j12] = g2[1 + k1];
σy[(ne-1)*4+j13] = g2[3 + k2];
σy[(ne-1)*4+j14] = g2[2 + k2];
}
//⑧「応力勾配と節点応力の大小」の図表らん(1)下
if( (j12==j21 && aC>(aA+Math.abs(aA*0.0000001))) || (j11==j22 && aC<(aA-Math.abs(aA*0.0000001))) ){
k1 = 0; k2 = 0; // 図表らん(3)
if(aB<aA){ k1 = 2; k2 = 2-4; } // 図表らん(4)
//⑨大小関係・図表の順位に並び換え
σy[(ne-1)*4+j11] = g2[1 + k1];
σy[(ne-1)*4+j12] = g2[0 + k1];
σy[(ne-1)*4+j13] = g2[2 + k2];
σy[(ne-1)*4+j14] = g2[3 + k2];
}
//⑥応力τxyについて
aA = τxy_av[ne]; aB = τxy_av[n1]; aC = τxy_av[n2];
for(i=1;i<=4;i++){g1[(i-1)] = τxy[(ne-1)*4+i];}
MaxA(); //⑦
//⑧ 図表らん(2)
if( Math.abs(aB- aA)< Math.abs(aC- aA)){
a = g2[1]; g2[1]= g2[2]; g2[2] =a;
}
j23 = j22 +1; if(j22>3){j23 = j22 +1-4;}
j13 = j12 +1; if(j12>3){j13 = j12 +1-4;}
j14 = j12 +2; if(j12>2){j14 = j12 +2-4;}
//⑧ 図表らん(1)上
if( (j12==j21 && aC<(aA-Math.abs(aA*0.0000001))) || (j11==j22 && aC>(aA+Math.abs(aA*0.0000001))) ){
k1 = 0; k2 = 0;
if(aB<aA){ k1 = 2; k2 = 2-4; }
//⑨大小関係・図表の順位に並び換え
τxy[(ne-1)*4+j11] = g2[0 + k1];
τxy[(ne-1)*4+j12] = g2[1 + k1];
τxy[(ne-1)*4+j13] = g2[3 + k2];
τxy[(ne-1)*4+j14] = g2[2 + k2];
}
//⑧ 図表らん(1)下
if( (j12==j21 && aC>(aA+Math.abs(aA*0.0000001))) || (j11==j22 && aC<(aA-Math.abs(aA*0.0000001))) ){
k1 = 0; k2 = 0; // 図表らん(3)
if(aB<aA){ k1 = 2; k2 = 2-4; } // 図表らん(4)
//⑨大小関係・図表の順位に並び換え
τxy[(ne-1)*4+j11] = g2[1 + k1];
τxy[(ne-1)*4+j12] = g2[0 + k1];
τxy[(ne-1)*4+j13] = g2[2 + k2];
τxy[(ne-1)*4+j14] = g2[3 + k2];
}
}
}
//---------計算結果の画面出力--------
var dc2= "";
dc2 += "*処理前と処理後の節点応力<br>";
dc2 += "<nobr> 要素-(k) 節点 σx(前) σy(前) τxy(前) σx(後) σy(後) τxy(後)</nobr><br>";
for( ne=1;ne<=NELT;ne++){
for( k=1;k<=4;k++){
dc2 += "<nobr> "+(ne)+" - ("+k+") "+(NodNo[(ne-1)*4+k]);
dc2 += " "+ dsp(σx_org[(ne-1)*4+k],5)+" "+dsp(σy_org[(ne-1)*4+k],5)+" "+dsp(τxy_org[(ne-1)*4+k],5);
dc2 += " "+ dsp(σx[(ne-1)*4+k],5)+" "+ dsp(σy[(ne-1)*4+k],5)+" "+ dsp(τxy[(ne-1)*4+k],5);
dc2 += " </nobr><br>";
}}
document.getElementById("results").innerHTML= dc2;
}
g1 = new Array(3);
g2 = new Array(3);
function MaxA(){
//⑦ 応力値:g1[n]、但しn=0~3。この4個の応力値a,b,c,dを大の順にソート、その順位の応力値=g2[順位]
if(g1[0]>g1[1]){ g2[0] = g1[0]; g2[1] = g1[1];}
else{g2[0] = g1[1]; g2[1] = g1[0];}
if(g1[2]>g2[0]){g2[2] = g2[1]; g2[1] = g2[0]; g2[0] = g1[2];}
else if(g1[2]>g2[1]){g2[2] = g2[1]; g2[1] = g1[2]; }
else {g2[2] = g1[2];}
if(g1[3]>g2[0]){g2[3] = g2[2]; g2[2] = g2[1]; g2[1] = g2[0]; g2[0] = g1[3];}
else if(g1[3]>g2[1]){g2[3] = g2[2]; g2[2] = g2[1]; g2[1] = g1[3];}
else if(g1[3]>g2[2]){g2[3] = g2[2]; g2[2] = g1[3];}
else{g2[3] = g1[3];}
}
function dsp(a,b){
aa = a + "";
if((b-aa.length)==1){aa = aa +"0";}
if((b-aa.length)==2){aa = aa +"00";}
return(aa);
}
//-->
</script>
</head>
<BODY onLoad='Node_Stress()'>
<div id="results"></div><br>
</body>
</HTML>
|
■プログラム出力 (上記サンプル例①②での計算結果)
|
*処理前と処理後の節点応力値
要素-(k) 節点 σx(前) σy(前) τxy(前) σx(後) σy(後) τxy(後)
1 - (1) 1 -21.0 79.00 33.00 -34.0 83.00 17.00
1 - (2) 2 -34.0 16.00 42.00 -11.0 20.00 42.00
1 - (3) 5 -11.0 20.00 17.00 2.000 16.00 33.00
1 - (4) 4 2.000 83.00 8.000 -21.0 79.00 8.000
2 - (1) 2 34.00 -16.0 42.00 11.00 -20.0 33.00
2 - (2) 3 21.00 -79.0 33.00 34.00 -83.0 8.000
2 - (3) 6 -2.00 -83.0 8.000 21.00 -79.0 17.00
2 - (4) 5 11.00 -20.0 17.00 -2.00 -16.0 42.00
3 - (1) 4 6.000 24.00 24.00 6.000 29.00 33.00
3 - (2) 5 3.000 7.000 33.00 3.000 11.00 26.00
3 - (3) 8 25.00 11.00 26.00 25.00 7.000 17.00
3 - (4) 7 29.00 29.00 17.00 29.00 24.00 24.00
4 - (1) 5 -3.00 -7.00 33.00 -3.00 -11.0 33.00
4 - (2) 6 -6.00 -24.0 24.00 -6.00 -29.0 26.00
4 - (3) 9 -29.0 -29.0 17.00 -29.0 -24.0 17.00
4 - (4) 8 -25.0 -11.0 26.00 -25.0 -7.00 24.00
| 
|
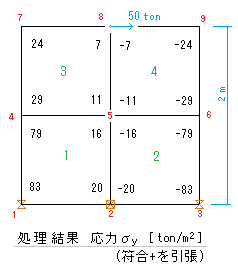
上記結果のσyについて、節点について算出すると、
節点No σy
1: σy=83
2: σy=(-20+20)/2=0
3: σy=-83
4: σy=(79+29)/2=54
5: σy=(16-16+11-11)/2=0
6: σy=(-79-29)/2=-54
7: σy=24
8: σy=(7-7)/2=0
9: σy=-24
従って、σyの最大値は、底面の両端(節点No1,3)に生じ、{σy}max = ±83 となる。
上記に用いているモデル例に関し、応力値σyの最大値は、下記表の如くの結果となった。
| 要素数 | 節点数 |
平均応力 (誤差) | 節点応力 (誤差) |
計算時間 | 誤差比較 |
| 4 | 9 |
49 (-67 %) | 83 (-44 %) |
0.1 秒 |
平均の応力値については、要素数400で 誤差1割以下
節点の応力値については、要素数100で 誤差1割以下
なお、
平均は、要素に於けるガウス積分で得られた値の平均
|
| 100 | 121 |
132 (-12 %) | 145 ( -3 %) |
0.5 秒 |
| 400 | 441 |
145 ( -3 %) | 153 ( 2 %) |
3.0 秒 |
| 1600 | 1681 |
152 ( 2 %) | 156 ( 4 %) |
32.0 秒 |
本例では要素数1600未満に於いて、単なる平均応力値よりも、配置処理による節点応力値が優れている。
なお、
・応力値の単位 [ton/m2]
・応力の理論値 σy= M/Z= 150 ton/m2、ここに M= F・L= 50x2= 100 ton・m、Z= B・H2/6= 1x22/6= 2/3 m3
・計算ソフトは JavaScript、ブラウザをIE9(32bit)、データをcsvファイルとした。

