構造力学・強度計算実践への一歩 板計算の説明（有限要素法）	2013-04-28　Mori design office
概要：有限要素法による、板の変位･モーメント･応力の計算式(A項)、及び算出方法を説明します(B項)。 計算結果を収束性を含めて考察し、 　　　および特異例として梁理論値、円板理論値と比較検証します(C項)。 最後に、計算式を誘導する為の理論と手順を述べます(D項)。 → 板計算の画面(FEM)

A. 計算式

・ここでの有限要素法(FEM)は、ACMと呼ばれる矩形の要素で計算を行う。 板を複数の要素に分割する。 　１つの要素(矩形)において、 横長2a、縦長2ｂとして 次の剛性方程式が成立し、頂点(節点)の 　変位･角度(δ,θX,θY)に対し、頂点に作用する外力が算出できる式となっている。 　　剛性方程式 　 　　[Ｋ]{ω} = {Ｆ}12x12　　12x1　　　　　12x1 　　　　　---(A1) 　 　　ここに、

変位ベクトル を{ω}とし、要素の頂点 1,2,3,4 における、ｚ方向変位δZと x,yに対する角度θX,θYのベクトルとなっている。 　　{ω} = [δZ1　θX1　θY1 　δZ2　θX2　θY2 　δZ3　θX3　θY3 　δZ4　θX4　θY4 ]T　 ---(A2) 　 　　外力ベクトル を{Ｆ}とし、要素の頂点 1,2,3,4 に作用する、z方向力fとモーメントmのベクトルとなっている。 　　{Ｆ} = [ f1　 mX1　 mY1 　 f2　 mX2　 mY2 　 f3　 mX3　 mY3 　 f4　 mX4　 mY4 ]T　　 ---(A3) 　　なお、 　　モーメントの方向は、例えば mX は ３次元でのmY であり、Y軸中心回転（右手法則)とする。 　　モーメントMは、板理論で用いられている、単位長さ当たりのモーメントとする。 　　　　 　mX1 =　bMX1 　mX2 = -bMX2 　mX3 = -bMX3 　mX4 =　bMX4 　　　　 　mY1 =　aMY1 　mY2 =　aMY2 　mY3 = -aMY3 　mY4 = -aMY4 　　 ---(A4)

要素剛性行列 を[Ｋ]とし、この構成は 12x12の対称行列で、各要素は下記の如くになっている。

K01,01 = D(10a4+10b4+(7-2ν)a2b2)/(10a3b3) K01,02 = D((1+4ν)a2+10b2)/(10a2b) K01,03 = D(10a2+(1+4ν)b2)/(10ab2)	[kgf/m] [kgf] [kgf]
K01,04 = D(5a4-10b4-(7-2ν)a2b2)/(10a3b3) K01,05 = D((1-ν)a2+10b2)/(10a2b) K01,06 = D(5a2-(1+4ν)b2)/(10ab2)	[kgf/m] [kgf] [kgf]
K01,07 = D(-5a4-5b4+(7-2ν)a2b2)/(10a3b3) K01,08 = -D((1-ν)a2-5b2)/(10a2b) K01,9 = D(5a2-(1-ν)b2)/(10ab2)	[kgf/m] [kgf] [kgf]
K01,10 = D(-10a4+5b4-(7-2ν)a2b2)/(10a3b3) K01,11 = D(-(1+4*ν)a2+5b2)/(10a2b) K01,12 = D(10a2+(1-ν)b2)/(10ab2)	[kgf/m] [kgf] [kgf]
K02,01 = K01,02 K02,02 = D(4(1-ν)a2+20b2)/(15ab) K02,03 = Dν	[kgf] [kgf･m] [kgf･m]
K02,04 = -D((1-ν)a2+10b2)/(10a2b) K02,05 = D(-(1-ν)a2+10b2)/(15ab) K02,06 = 0	[kgf] [kgf･m] [kgf･m]
K02,07 = -D(-(1-ν)a2+5b2)/(10a2b) K02,08 = D((1-ν)a2+5b2)/(15ab) K02,09 = 0	[kgf] [kgf･m] [kgf･m]
K02,10 = D(-(1+4*ν)a2+5b2)/(10a2b) K02,11 = D(-4*(1-ν)a2+10b2)/(15ab) K02,12 = 0	[kgf] [kgf･m] [kgf･m]
K03,01 = K01,03 K03,02 = K02,03 K03,03 = D(20a2+4*(1-ν)b2)/(15ab)	[kgf] [kgf･m] [kgf･m]
K03,04 = D(5a2-(1+ 4ν)b2)/(10ab2) K03,05 = 0 K03,06 = D(10a2-(4-4ν)b2)/(15ab)	[kgf] [kgf･m] [kgf･m]
K03,07 = D(-5a2+(1-ν)b2)/(10ab2) K03,08 = 0 K03,09 = D(5a2+(1-ν)b2)/(15ab)	[kgf] [kgf･m] [kgf･m]
K03,10 = -D(10a2+(1-ν)b2)/(10ab2) K03,11 = 0 K03,12 = D(10a2-(1-ν)b2)/(15ab)	[kgf] [kgf･m] [kgf･m]
･･･ ･･･中略 ･･･ K10,10 = D(10a4+10b4+(7-2ν)a2b2)/(10a3b3) K10,11 = D((1+4ν)a2+10b2)/(10a2b) K10,12 = D(-10a2-(1+4ν)b2)/(10ab2)	[kgf/m] [kgf] [kgf]
K11,10 = K10,11 K11,11 = D(8(1-ν)a2+40b2)/(30ab) K11,12 = -Dν	[kgf] [kgf･m] [kgf･m]
K12,10 = K10,12 K12,11 = K11,12 K12,12 = D(20a2+4(1-ν)b2)/(15ab) 　 なお、 板の曲げ剛性　D = Eh3/(12(1-ν2))	[kgf] [kgf･m] [kgf･m] 　 　 　 [kgf･m]

★モーメントが一般の定義、または単位長さ当たりかの明確な記述にて、単位を参考付記してます。 　　　変位：δ[m]　　角度：θ[rad]　　力：f[kgf]　　モーメント：m[kgf･m]　　モーメント：M[kgf] 　　　(但し、上記の記述 キログラム重量 kgf 総てに対し、SI単位系では kgfを ニュートン N に読替えて下さい。)

B. 計算方法 (プログラミングへの要約)

既知外力より変位を算出する手順を述べる。ここでは、外部モーメントは板の外周のみ作用するとする。 　　�@12元連立方程式 　　　上記式(A1)を全要素に適用させる。連立式は、要素数の12倍の数となる。 　　�A組立合成(全体剛性行列) 　　　共通節点のは加算合成して、節点総数に対する式を得る。 　　　例えば、板の区割り数を横ia、縦ib の場合 　　　　要素総数Nelt=ia･ib、節点総数Nnod =(ia+1)･(ib+1) 　　　　全要素 に式(A1)を適応させると、連立式数Nelt x 3 であり、 　　　　共通節点のは加算合成で、連立式数 Nnodｘ3となる。 　　　・外周のモーメント 　　　　板の辺a全にMy、辺b全にMxが作用する場合、 　　　　要素毎に計算、式(A4)を計算する。 　　　　節点に作用するモーメントが、2個の要素にまたがるばあいは、各々要素に対し1/2づづにする 。 　　　　この値を外力{Ｆ}に代入する。 　　�B変位の既知処理 　　　変位に関し、既に既知である場合、連立式から除外する。 　　　・例：境界条件は支持方法であり、下記の既知節点処理となる。 　　　　・全周単純支持では、変位z=0の既知であり、既知節点数 No = 2(ia+ib)だけを除外して 　　　　　連立式数は Nnodｘ3 - 2(ia+ib) 　　　　・全周固定支持では、θx=0,θy=0の既知も加わる故、 No = 2(ia+ib)･3 個の式を除外して 　　　　　連立式数 Nnodｘ3 - 2(ia+ib)ｘ3　のを解くことになる。 　　　・強制変位δzの場合 　　　　　変位δzに相当の力 {Fz} = [Ｋ]{δ} 算出する。 　　　　　外力Ｆと相殺して、{Fo} = {Ｆ} - {Fz}　を算出する。 　　　　　全剛性式 [Ｋ]{ω} = {Fo}　であり、上述と同様に既知節点を除外して、連立式を立てる。 　　　・この既知節点除外のプログラミングは、 　　　　　例えば、既知節点が1,2,3,･･のKOZ個の場合、既知節点配列をknow[0,1,2,3,･･]とすると、 　　　　　for(i=1;i<=Nnod3;i++){index[i]=1;} のパラメータに for(i=1;i<=KOZ;i++){index[know[i]]=0;} 　　　　　m = 0; for(i=1;i<= Nnod3;i++){ if (index[i]>0){ m = m + 1; index[m] = i;} } 　　　　　for(i=1;i<= m;i++){ F[i] = F[index[i]]; 　　　　　　　for(j=1;j<= m;j++){K[(i-1)*index[i]+ j] = K[(index[i]-1)*Nnod3+ index[j]];} 　　　　　} 　　　・これにて、求めるべき式 [Ｋ]{ω} = {Ｆ}の Ｋ,Ｆが得られたことになる。 　　�C連立式の解法 　　　・得られた [Ｋ]は正方行列mxmで、逆行列 [Ｋ]-1 で変位ωが求められる。 　　　・プログラミングとしては、ガウスジョルダン法やコレスキー法などがある。 　　　・この方法は、処理結果が外力F[i]の場所に変位の値が出る。即ち、F[i]＝変位の値 に置換される。 　　�D変位{ω}の算出 　　　・�Cで得られた値に対し、�Bの既知処理の逆処理を行う 　　　　for(i=1;i<=Nnod3;i++){ω[i] = 0;} 　　　　for(i=1;i<=mm;i++){ω[index[i]] = F[i];} 　　　　for(i=1;i<=Nnod3;i++){ ω[i] = ω[i] + 強制変位δ[i]; } 　　�E内力の算出 　　　・変位の値が算出できたので、各要素ごとに剛性方程式(A1)に代入して内力F及びモーメントMが算出できる。 　　　・算出した内力は、各々節点に関し単純加算して、節点の内力値を算出する。 　　　・モーメントは、式(A4)を参照して正負符号も含めて、単純平均でMx,Myを算出 　　　　(例えば同一節点が２個あれば、その合計値を２で割り単純平均)する。 　　　・応力 σx= 6Mx/h2　σy= 6My/h2

　

C.計算結果 (精度検証)

一般荷重での収束性 　　下記(a)〜(d)は、収束性が良く、要素数1600で便覧値に近い。 　　(a)全周単純支持：矩形板 横100cm x 縦100cm x 厚1cm、全面1000kgf 要素数 [個] 4 16 100 400 1600 便覧値 中央変位δ[cm] 0.101 0.205 0.210 0.211 0.211 0.211 中央Mx,My[kgf] 43.03 46.96 47.75 47.85 47.88 47.9 　　(b)全周固定：矩形板 横100cm x 縦100cm x 厚1cm　、全面1000kgf 要素数 [個] 4 16 100 400 1600 便覧値 中央変位δ[cm] 0.0655 0.0769 0.0730 0.0671 0.0661 0.0659 右辺中Mx [kgf] -25.33 -43.23 -50.14 -51.04 -51.26 -51.30 上辺中My [kgf] -25.33 -43.23 -50.14 -51.04 -51.26 -51.30 中央Mx　 [kgf] 28.8 25.36 23.36 23.02 22.93 23.10 中央My　 [kgf] 28.8 25.36 23.36 23.02 22.93 23.10 　　(c)全周固定：矩形板 横100cm x 縦200cm x 厚1cm　、全面1000kgf 要素数 [個] 4 16 100 400 1600 便覧値 中央変位δ[cm] 0.0831 0.0722 0.06687 0.06611 0.06589 0.0660 右辺中Mx [kgf] -26.00 -39.11 -41.19 -41.37 -41.42 -41.45 上辺中My [kgf] -8.18 -17.11 -26.18 -27.90 -28.35 -28.55 中央Mx　 [kgf] 27.0 23.49 21.12 20.71 20.61 20.61 中央My　 [kgf] 28.8 25.36 23.36 7.885 7.90 7.899 　　ポアソン比ν 　　(d)片持ち梁(はり)：30cmL x 1cmW x 3cmT　　先端F=-100kgf 条件 根元 先端 σx [kgf/cm2] σy [kgf/cm2] θx[°] θy[°] δz[cm] 要素数2740 　(10x274) ν=0.3 2408.583 697.777 -0.544353 0.00000 -0.189788 ν=0 1999.994 0.00000 -0.545679 0.00000 -0.190479 はり理論 ν=0 2000.000 ― -0.545674 ― -0.190476 　　･ポアソン比 ν=0 で 梁の理論値と５桁まで合致し、略同一値となっている。 　　･実際は、ν=0.3(鉄鋼)の故、応力値が理論値の２割増しが推測される。 　　☆はり理論：長さa=30cm、幅b=1cm、断面2次モーメント I = b･T3/12 = 2.25cm4 　　　　　　　　断面係数 Z = b･T2/6 = 1.5cm3 　　　　　　　　θ=F・a2/(2EI)、δ=F・a2/(3EI)、σ=-F・a/Z 　 　　モーメント 　　(e)片持ち梁(はり)：30cmL x 1cmW x 3cmT　先端Mx=100kgf(幅1cm当たり)　ν=0 要素数 [個] 400 (20x20) 3000 (100x30) 3000 (30x100) はり理論 Mx[kgf] 根元 103.991 103.312 99.434 100.000 先端 100.000 100.000 100.000 100.000 My[kgf] 根元 0.000 0.000 0.000 ― 先端 2.396 0.7874 0.0262 ― 先端変位δ[cm] -0.01039 -0.00984 -0.00953 -0.00952 　　･外力がモーメントの場合は、荷重の場合に比べ収束性が悪い。 　　･このモーメントの場合は、幅(1cm)の分割を多く(100)の方が精度が高い。 　 　　参考 　　(f)円形板： φ100cm x 厚1cm　全面1000kgf 円周の条件 単純支持 固定 計算条件 要素数 420 理論値 要素数 420 要素数 760 理論値 中央変位δ[cm] 　0.267 　0.264 　 0.068 　 0.068 　 0.065 中央Mx　[kgf] 　67.6 　65.7 　 27.4 　 26.9 　 25.9 中央My　[kgf] 　67.6 　65.7 　 27.4 　 26.9 　 25.9 右端Mx　[kgf] 　0.00 　0.00 　-41.5 　-41.4 　-39.8 右端My　[kgf] 　34.3 　39.8 　-13.5 　-13.7 　-11.9 　　・計算のモデルは、円周部の要素の対角に支持を配設していて、精度が低い。 　　　分割数を大きくするほど、円周部のモーメント値に乱れが大きくなる。 　 　　(g)典型的条件に条件追加によるプログラムチェック（数値およびグラフ割愛） 　　　 全周単純支持の条件に 　　　　・左右辺において、θy=0 及び　Mx=全周固定での値 　　　　・上下辺において、θx=0 及び　My=全周固定での値 　　　　結果値は、全周固定の条件と同一となる。 　 　　　 荷重零の条件に 　　　　・変位δ＝集中荷重が有りでの変位 　　　　　（集中荷重の点を 変位拘束点として) 　　　　結果値は、集中荷重が既知で 荷重下位置が変位未知の場合 と同一となる。 　　　などが考えられる。

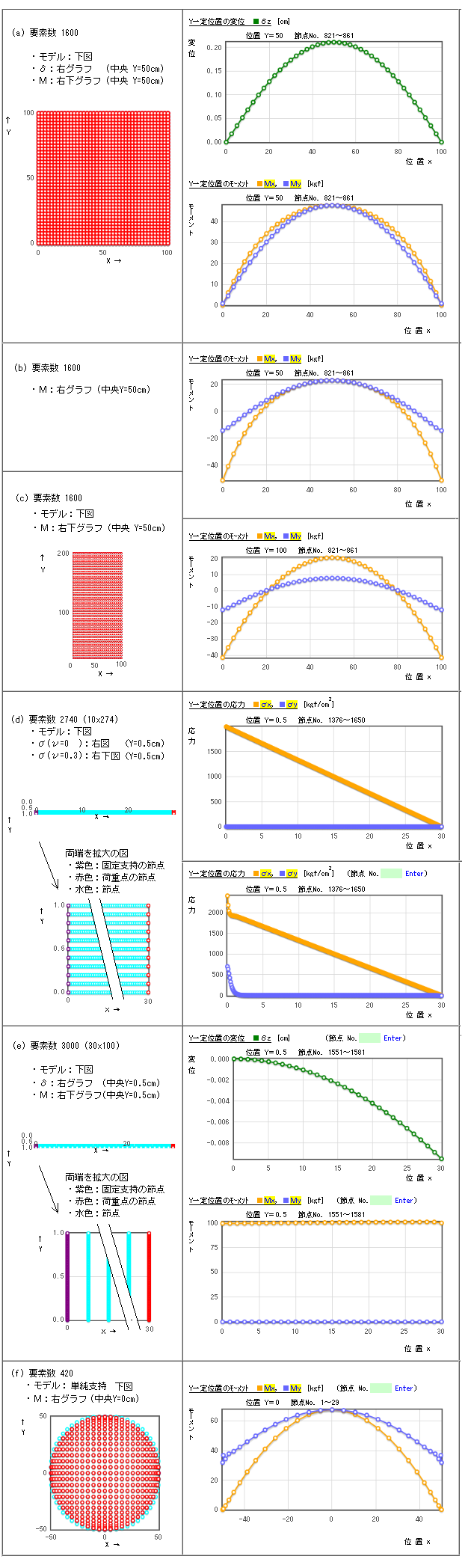
使用した物理定数値 　　ポアソン比 ν= 0.3 　　ヤング率　 E= 2100000 [kgf/cm2] 　　　　　　 （ SI単位系: 2.06e+11N/m2, 206Gpa )

　

D.理論 (式の誘導)

近似多項式 四角形要素において、定数項α1〜α12を用いて、任意のたわみを近似多項式 　　ω(x,y) = {Ｐ}{α} ---(1) で記述する。ここに、 　　　 {Ｐ} = [ 1　ξ　η　ξ2　ξη　η2　ξ3　ξ2η　ξη2　η3　ξ3η　ξη3] ---(2) 　　　 {α} = [ α1　α2　α3　α4　α5　α6　α7　α8　α9　α10　α11　α12]T 　 これを、たわみω及び たわみ角度θx、θy に適応させて、{ω} = [Ｃ]{α} 12x12　 12x1 なお、 　　{ω} = [ω1　θx1　θy1　ω2　θx2　θy2　ω3　θx3　θy3　ω4　θx4　θy4]T ---(3) 　 ---(4) 　 ---(5) 　 　 　　各要素は、頂点１(ξ=-1,η=-1) では 　　　ω1 = p1 α1　+　p2 α2　+　p3 α3　+・・・+　p12α12 　　　θx1= 1 ∂p1 α1 + 1 ∂p2 α2 + 1 ∂p3 α3 + ･･･ + 1 ∂p12 α12 　　　　　　a ∂ξ 　　 a ∂ξ 　　 a ∂ξ 　　　　　 a ∂ξ 　　　θy1= 1 ∂p1 α1 + 1 ∂p2 α2 + 1 ∂p3 α3 + ･･･ + 1 ∂p12 α12 　　　　　　b ∂η 　　 b ∂η 　　 b ∂η 　　　　　 b ∂η ---(6) 　 　　頂点2 (ξ=1,η=-1)、頂点3 (ξ=1,η=1)、頂点4 (ξ=-1,η=1) も同様で 　　例えば 頂点4 の θy4 は 　　　θy4= 1 ∂p1 α1 + 1 ∂p2 α2 + 1 ∂p3 α3 + ･･･ + 1 ∂p12 α12 　　　　　　b ∂η 　　 b ∂η 　　 b ∂η 　　　　　 b ∂η ---(6)' 　　なお、記述簡易にて {Ｐ}の要素kを pk と記した。 　 　 内挿関数Ｎ 変位を　ω(x,y) = {Ｎk}{α} とし、上記式(1)(4)(6)より各要素は下記となる。 　　N1 = -((η+1)η+(ξ+2)(ξ-1))(η-1)(ξ-1)/8 　　N2 = -(η-1)(ξ+1)(ξ-1)2a/8 　　N3 = -(η+1)(η-1)2(ξ-1)b/8 　　N4 = ((η+1)η+(ξ+1)(ξ-2))(η-1)(ξ+1)/8 　　N5 = -(η-1)(ξ+1)2(ξ-1)a/8 　　N6 = (η+1)(η-1)2(ξ+1)b/8 　　N7 = -((η+1)η+(ξ+1)(ξ-2))(η+1)(ξ+1)/8 　　N8 = (η+1)(ξ+1)2(ξ-1)a/8 　　N9 = (η+1)2(η-1)(ξ+1)b/8 　　N10= ((η-1)η+(ξ+2)(ξ-1))(η+1)(ξ-1)/8 　　N11= (η+1)(ξ+1)(ξ-1)2a/8 　　N12= -(η+1)2(η-1)(ξ-1)b/8 ---(7) 歪は、上記の内挿関数を用いて次のようになる。 　　{ε} = [Ｂ]{ω}3x12　　12x1 　 　　　ここに、 　　　　 {ε} = [ -∂2ω　　-∂2ω　　- ∂2ω 　]T 　　　　　　　　　 ∂x2 　　 ∂y2 　　 ∂y∂x 　　　及び ---(8) 　 　 　 ---(9) ╭ ╰ [Ｂ] =　 　-∂2N1　　-∂2N2　　-∂2N3 　･･･ -∂2N12 　∂x2 　　 ∂x2 　　 ∂x2 　　　 　∂x2 　-∂2N1　　-∂2N2　　-∂2N3 　･･･ -∂2N12 　∂y2 　　 ∂y2 　　 ∂y2 　　　 　∂y2 　- ∂2N1　 - ∂2N2　 - ∂2N3 ･･･ -　∂2N12 　∂x∂y 　∂x∂y 　∂x∂y 　　 ∂x∂y ╮ ╯ ---(10) 　 　 さて、力の釣り合いの式は、仮想原理もしくはエネルギー最小化原理にて、 　　[Ｋ]{ω} = {Ｆ}12x12　　12x1　　　　　12x1 ---(11) 　　　　ここに、{Ｆ} は、外力ベクトル、[Ｋ] は、要素剛性マトリックスとなっている。 　 　　　　[Ｋ] = ∫b-b ∫a-a [Ｂ]T[Ｄ][Ｂ]dxdy = ab ∫1-1 ∫1-1 [Ｂ]T[Ｄ][Ｂ]dξdη ---(12) ╭ [Ｄ] =　D ╰ 　 1　　ν　　0　　 　 ν　 1　　 0　　 　 0　　0　 (1-ν)/2 ╮ ╯ ---(13) 　　　　D = 　　Eh3 　　　　　　12(1-ν )2 　　　　なお、マトリックス[Ｄ]は弾性定数、D は板の曲げ剛性、Eはヤング率である。 　 　 要素剛性行列の誘導計算 内挿関数{Nk}の式(7)を式(10)(12)に順次代入して、前述の(A5)が求められる。 この計算に必要なＮの変微分は式(7)より下記の如くとなっている。 ∂2N1 /∂ξ2= -3ξ(η-1)/4 ∂2N1 /∂η2= -3(ξ-1)η/4 ∂2N1 /∂ξ∂η= -(3ξ2+3η2-4)/8 ∂2N2 /∂ξ2= -a(3ξ-1)(η-1)/4 ∂2N2 /∂η2= 0 ∂2N2 /∂ξ∂η= -a(3ξ2-2ξ-1)/8 ∂2N3 /∂ξ2= 0 ∂2N3 /∂η2= -b(ξ-1)(3η-1)/4 ∂2N3 /∂ξ∂η= -b(3η2-2η-1)/8 ∂2N4 /∂ξ2= 3ξ(η-1)/4 ∂2N4 /∂η2= 3(ξ+1)η/4 ∂2N4 /∂ξ∂η= (3ξ2+3η2-4)/8 ∂2N5 /∂ξ2= -a(3ξ+1)(η-1)/4 ∂2N5 /∂η2= 0 ∂2N5 /∂ξ∂η= -a(3ξ2+2ξ-1)/8 ∂2N6 /∂ξ2= 0 ∂2N6 /∂η2= b(ξ+1)(3η-1)/4 ∂2N6 /∂ξ∂η= b(3η2-2η-1)/8 ∂2N7 /∂ξ2= -3ξ(η+1)/4 ∂2N7 /∂η2= -3(ξ+1)η/4 ∂2N7 /∂ξ∂η= -(3ξ2+3η2-4)/8 ∂2N8 /∂ξ2= a(3ξ+1)(η+1)/4 ∂2N8 /∂η2= 0 ∂2N8 /∂ξ∂η= -a(3ξ2+2ξ-1)/8 ∂2N9 /∂ξ2= 0 ∂2N9 /∂η2= b(ξ+1)(3η+1)/4 ∂2N9 /∂ξ∂η= b(3η2+2η-1)/8 ∂2N10 /∂ξ2= 3ξ(η+1)/4 ∂2N10 /∂η2= 3(ξ-1)η/4 ∂2N10 /∂ξ∂η= (3ξ2+3η2-4)/8 ∂2N11 /∂ξ2= a(3ξ-1)(η+1)/4 ∂2N11 /∂η2= 0 ∂2N11 /∂ξ∂η= a(3ξ2-2ξ-1)/8 ∂2N12 /∂ξ2= 0 ∂2N12 /∂η2= -b(ξ-1)(3η+1)/4 ∂2N12 /∂ξ∂η= -b(3η2+2η-1)/8 ・板の関連資料：板計算説明(級数) 　FEMの関連：FEM要約(四角形)、 FEM入門(三角形) 　Copyright(C) Mori Design office 　All rights Reserved.